Classic Roulette Strategies
Roulette is a classic gambling game whose origins date back to 18^(th)-century France. The invention of the roulette wheel is traditionally attributed to Blaise Pascal, a French physicist and mathematician who, in the 17th century, attempted to create a perpetual motion machine. Although this experiment was not a success, it led to the creation of a device that would later inspire one of the world’s most famous casino games.
By the early 19th century, roulette had become a staple of European casinos, captivating players with its elegance, suspense and apparent simplicity. It spread rapidly from Paris to Monte Carlo and then across the Atlantic to America, where a modified wheel featuring a double zero was introduced, creating the distinction between European and American roulette. Over time, roulette has become a symbol of sophistication, chance and calculated risk — a game that is equally popular with mathematicians and gamblers.

Probability theory and classic strategies in roulette
The history of roulette is deeply intertwined with the development of probability theory. In 1654, Blaise Pascal and Pierre de Fermat exchanged a series of letters discussing the famous ‘problem of points’ — namely, how to divide stakes fairly in an unfinished game of chance. This correspondence laid the foundation for modern probability theory, forever linking gambling with mathematics. Although these discussions took place decades before roulette took its modern form, they established the principles of risk, expectation and randomness that underpin the game. As roulette spread throughout Europe in the 18^(th) and 19^(th) centuries, it became a model for developing various gaming strategies.

Martingale Strategy
The Martingale system is one of the oldest and most famous betting strategies in gambling history. It is believed to have originated in 18^(th)-century France, developed by mathematical enthusiasts fascinated by probability and games of chance. It gained further popularity thanks to John H. Martindale, a London casino owner from the same era who encouraged his patrons to ‘double their bets after losing’.
For nearly three centuries, the Martingale system has remained a simple yet intriguing betting approach. Its core idea can be summarised in seven words: if you lose, double your bet. The logic is straightforward: when you eventually win, that single win will recover all previous losses and provide a profit equal to your original wager.
This strategy’s appeal lies in its simplicity and mathematical clarity, and it can be applied to roulette as well as other casino games.
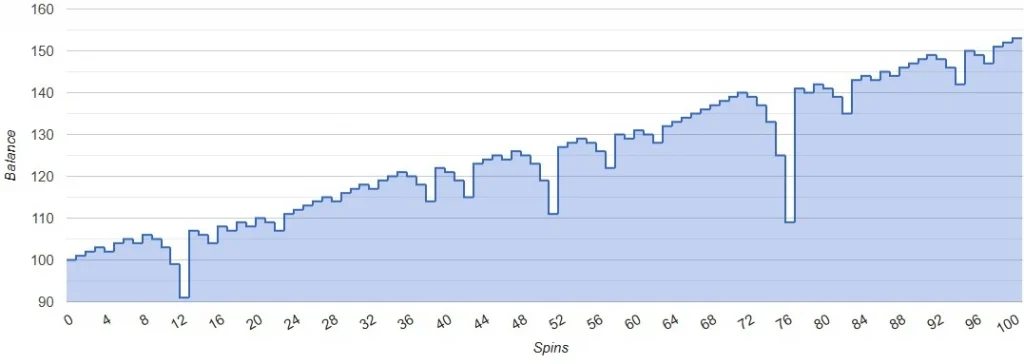
Martingale Strategy Simulation – positive scenario (Bet=1$, Balance=100$, Spins=100):
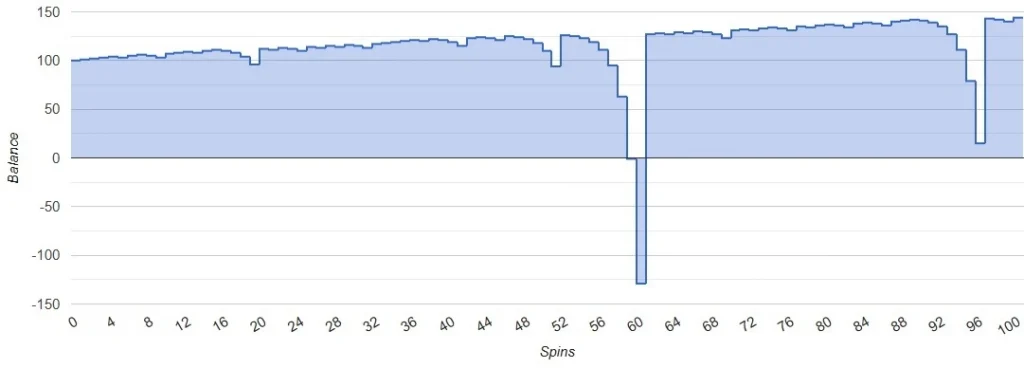
Martingale Strategy Simulation – negative scenario (Bet=1$, Balance=100$, Spins=100):
Fibonacci Strategy
The Fibonacci strategy in roulette is based on the numerical sequence of the same name. This mathematical pattern was discovered by the Italian mathematician Leonardo of Pisa, also known as Fibonacci, in the 13th century. The sequence starts with 1 and 1, and each number after that is the sum of the two numbers before it (1, 1, 2, 3, 5, 8, 13, and so on).
In roulette, this sequence is used to decide how much you bet next. After you lose, you move one step forward in the sequence and increase your next bet. If you win, you move two steps backward and bet less next time. The idea is to gradually recover previous losses while keeping bets small.
This system is similar to the Martingale strategy, as both are negative progression systems that increase bet size after losses. However, the Fibonacci approach is less extreme. Instead of doubling your bet every time, you increase your bet bit by bit following the sequence. This makes it safer when you’re not winning, but it might take longer to start making a profit again.
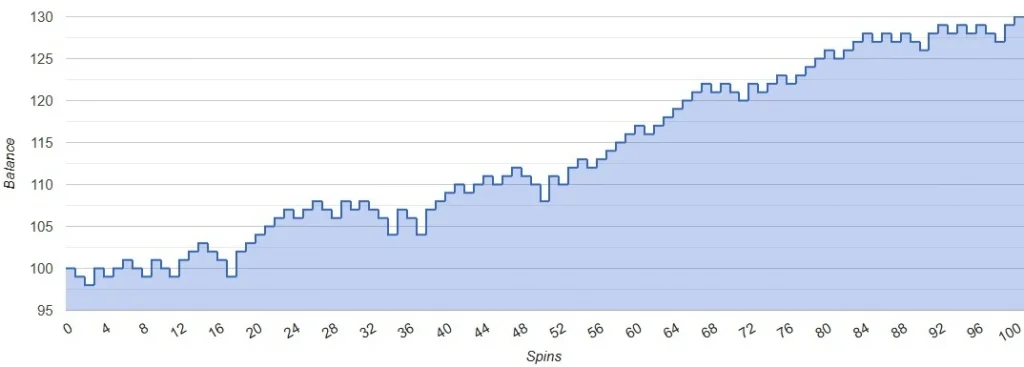
Fibonacci Strategy Simulation – positive scenario (Bet=1$, Balance=100$, Spins=100):
Fibonacci Strategy Simulation – negative scenario (Bet=1$, Balance=100$, Spins=100):
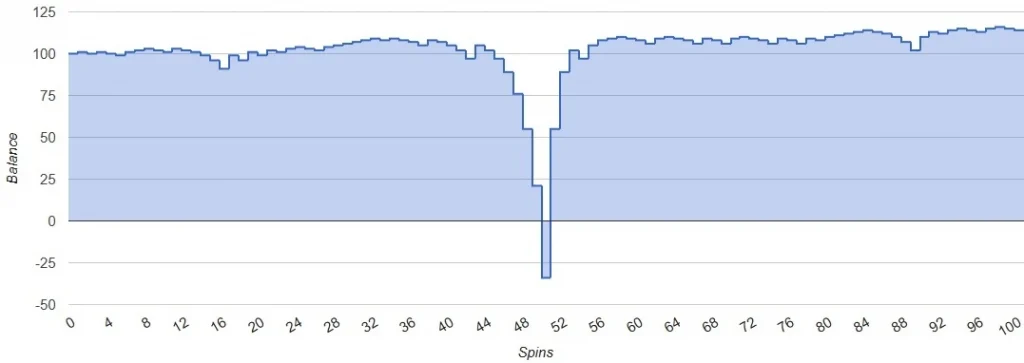
Labouchere System
The Labouchere system, also called the cancellation system, was invented by Henry Labouchere, a British aristocrat, politician and gambling enthusiast from the 19th century. This strategy lets players plan their bets in advance by setting a target profit and dividing it into smaller, easier-to-manage numbers — for example, 1, 2, 3, 2, 2, 1.
To play, you add the first and last numbers in your sequence to determine your bet. If you win, you cross off those two numbers. If you lose, you add the amount you just bet to the end of your list. The aim is to clear all the numbers, which will make you reach your target profit
The main advantage of the Labouchere strategy is its flexibility: you can customize the flow of your session by choosing your own sequence. The problem with negative progression systems is that you may have to place very large bets when you lose for a while. This can lead to big losses, which can cancel out all your previous wins.
D’Alembert Strategy
The D’Alembert system is one of the simplest and most balanced betting strategies in roulette. It is named after its creator, the 18^(th)-century French physicist, philosopher and mathematician Jean le Rond d’Alembert (1717–1783). The principle behind the system is straightforward: after a loss, you increase your bet by one unit; after a win, you decrease it by one unit.
This approach aims to create a smoother betting progression compared to more aggressive systems like Martingale.
However, the strategy is based on the misconception that, after a series of losses, a win is more likely — a concept related to the gambler’s fallacy. In reality, however, roulette outcomes are completely random: each spin is independent and the wheel has no memory.
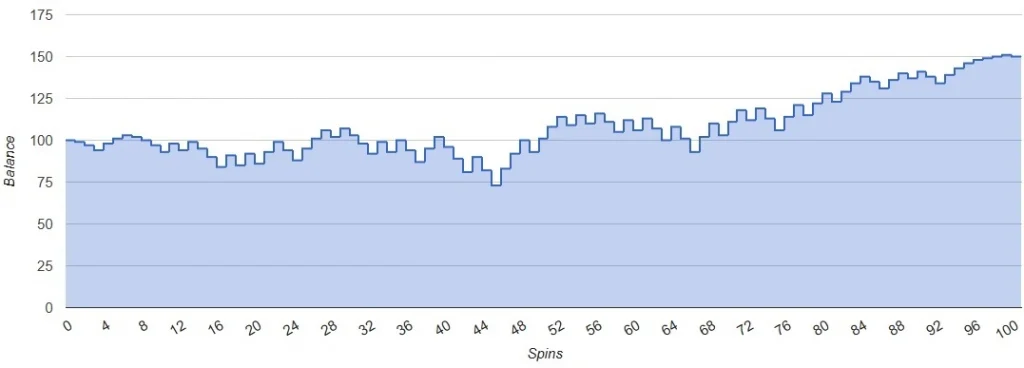
D’Alembert Strategy Simulation – positive scenario (Bet=1$, Balance=100$, Spins=100):
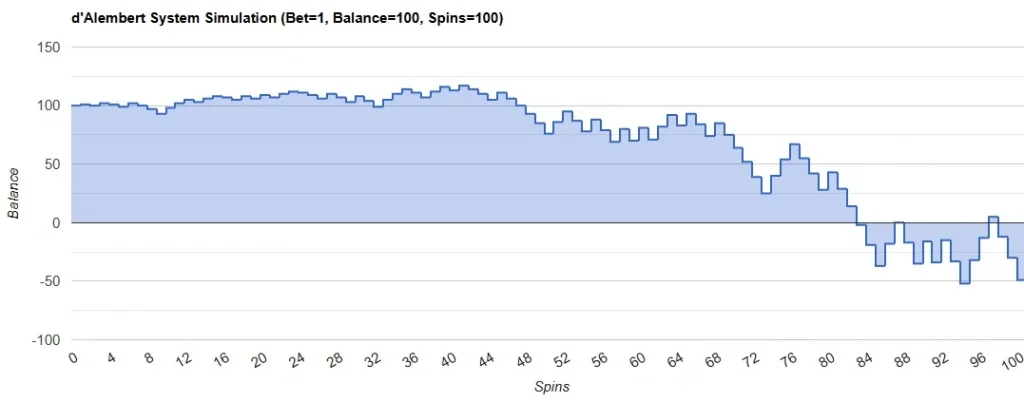
D’Alembert Strategy Simulation – negative scenario (Bet=1$, Balance=100$, Spins=100):
Oscar’s Strategy
The first person to describe this system was Allan N. Wilson, in his book “The Casino Gambler’s Guide”.
The idea is to increase your bet by one unit when you win and keep the same amount when you lose. Keep going until you start making a profit on your first bet. When you’re in the black, the sequence ends and you start over.
The system is based on the idea that you’re likely to win a small amount of money and it’s unlikely you’ll lose a lot. This means you can take your time and be careful to make a profit bit by bit. The aim of the system is to repeatedly win small, one-unit wins until you reach the amount you want to win. However, like all systems it is susceptible to the occasional devastating loss that will wipe out all of the previous small wins you might have achieved.
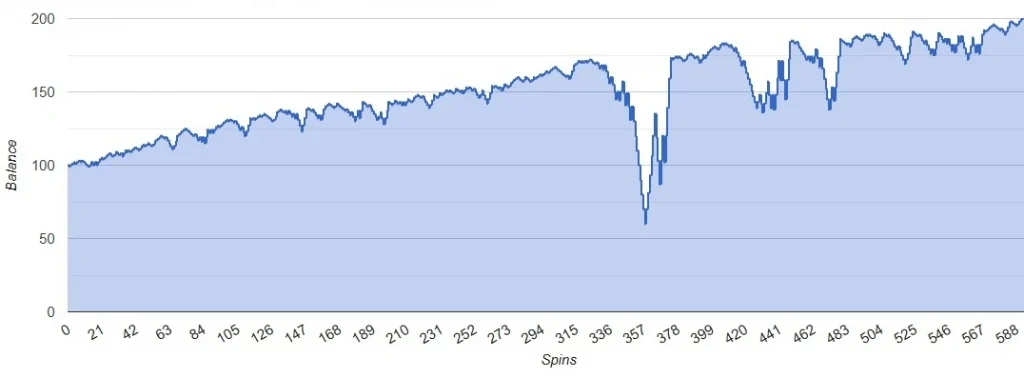
Oscar’s System Simulation – positive scenario (Bet=1$, Balance=100$, Repeat=100):
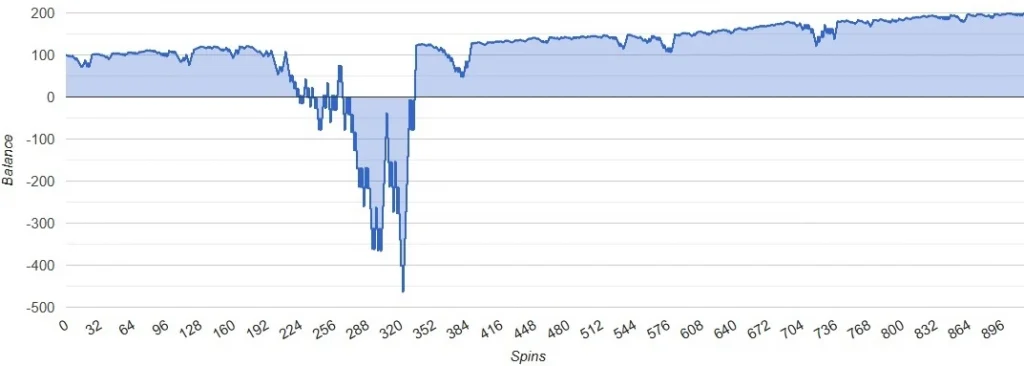
Oscar’s System Simulation – negative scenario (Bet=1$, Balance=100$, Repeat=100):
Conclusion
No system can guarantee consistent wins at roulette. The main advantage of using a betting system is that it helps you structure your bets consistently. However, systems with negative progressions, like the Martingale, can be risky — following them too rigidly can lead to significant losses. It’s important to remember that no matter the strategy, roulette is ultimately a game of chance. So, while systems can help manage your betting, there’s no foolproof method to win money 100% of the time. Always gamble responsibly.
